Computer Science A
Selection - Insertion Sort
Sorting and Searching Algorithms
Introduction
Searching and sorting are fundamental concepts in computer science that help us organize and access data.
- Searching algorithms allow us to locate specific elements within a dataset,
- Sorting algorithms rearrange data into a meaningful order, such as ascending or descending.
Searching Algorithms
Searching algorithms help us find a specific element within a dataset. There are two primary types of searching algorithms: linear search and binary search.
- Linear search is a simple algorithm that iterates through each element in a dataset until it finds the target value. This algorithm is easy to implement but can be slow for large datasets.
- Binary search is a more efficient algorithm that works on sorted datasets. It repeatedly divides the dataset in half and compares the target value with the middle element. This process continues until the target value is found or the dataset is empty.
Types of Sorting Algorithms
Sorting algorithms rearrange data into a specific order, such as ascending or descending. There are many sorting algorithms available, each with its unique characteristics and performance trade-offs.
- Bubble sort is a simple sorting algorithm that repeatedly swaps adjacent elements if they are in the wrong order. While easy to think about and implement, bubble sort is not efficient for large datasets.
- Selection sort (College Board Featured) is a simple sorting algorithm that repeatedly selects the smallest element from the unsorted portion of the dataset and places it at the beginning. While easy to implement, selection sort is not efficient for large datasets.
- Insertion sort (College Board Featured) is a simple sorting algorithm that builds the final sorted array one element at a time. It iterates through the dataset, removing one element and inserting it into the correct position in the sorted array. Insertion sort is efficient for small datasets but can be slow for large datasets.
- Merge sort (College Board Featured) is another popular sorting algorithm that uses a divide-and-conquer approach to sort elements. It divides the dataset into two halves, sorts them separately, and then merges them back together. Merge sort is stable and has a guaranteed worst-case time complexity of O(n log n).
- Quicksort is a more efficient sorting algorithm that uses a divide-and-conquer strategy to sort elements in place. It recursively partitions the dataset into smaller subarrays and sorts them independently. Quicksort is widely used in practice due to its speed and simplicity.
1. Selection Sort
Selection sort is a simple sorting algorithm that works by selecting the smallest (or largest, depending on sorting order) element from the list and swapping it with the first unsorted element. The algorithm then finds the second smallest element and swaps it with the second unsorted element, and continues in this way until the entire list is sorted. It is similar to bubble sort, but it is more efficient as it reduces the number of swaps.
public class SelectionSort {
public static void main(String[] args) {
int[] list = {28, 12, 18, 8, 30, 3, 17, 14};
System.out.println("Sorting process:");
for (int currentIndex = 0; currentIndex < list.length - 1; currentIndex++) {
int minIndex = currentIndex;
// Find the minimum element in the unsorted part
for (int i = currentIndex + 1; i < list.length; i++) {
if (list[i] < list[minIndex]) {
minIndex = i;
}
}
// Swap the current element with the minimum element
int temp = list[currentIndex];
list[currentIndex] = list[minIndex];
list[minIndex] = temp;
// Print the array after each swap
printArray(list);
}
System.out.println("\nFinal sorted list:");
printArray(list);
}
// Helper method to print the array
private static void printArray(int[] array) {
for (int num : array) {
System.out.print(num + " ");
}
System.out.println();
}
}
SelectionSort.main(new String[]{});
Sorting process:
3 12 18 8 30 28 17 14
3 8 18 12 30 28 17 14
3 8 12 18 30 28 17 14
3 8 12 14 30 28 17 18
3 8 12 14 17 28 30 18
3 8 12 14 17 18 30 28
3 8 12 14 17 18 28 30
Final sorted list:
3 8 12 14 17 18 28 30
Selection Analysis - Big O
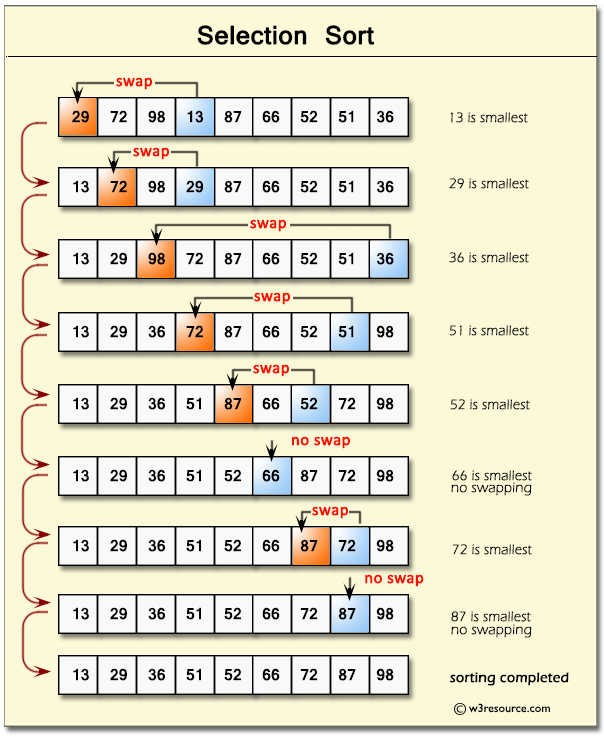
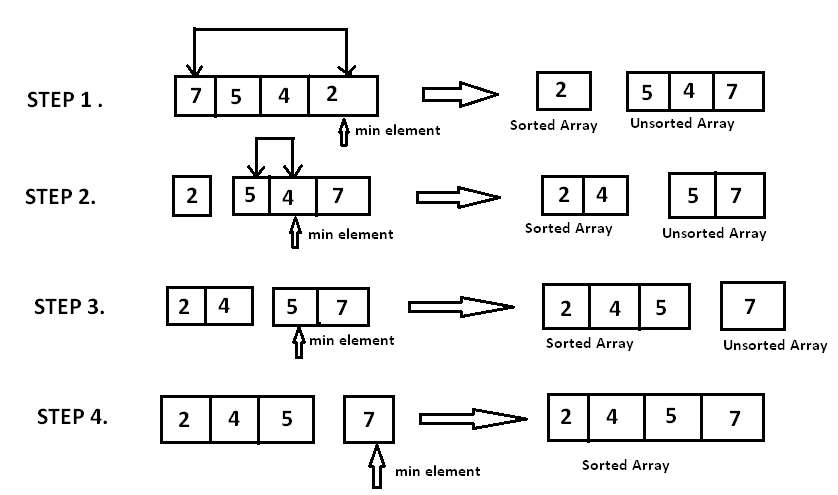
Let $n$ be the number of integers in an array.
Selection sort always performs the same number of comparisons, regardless of the initial order of the array.
Number of comparisons: $(n-1) + (n-2) + \ldots + 1 = \frac{n(n-1)}{2} \approx O(n^2)$
-
Best case: $O(n^2)$ (no improvement if array is already sorted).
-
Average case: $O(n^2)$ (elements are randomized).
-
Worst case: $O(n^2)$ (array is in reverse order; still the same number of comparisons).
2. Insertion Sort
Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort. However, insertion sort provides several advantages: simple implementation, efficient for (quite) small data sets, more efficient in practice than most other simple quadratic (i.e., O(n2)) algorithms such as selection sort or bubble sort, adaptive, stable, in-place, online, and can be made stable.
public class InsertionSort {
public static void main(String[] args) {
int[] list = {28, 12, 18, 8, 30, 3, 17, 14};
System.out.println("Sorting process:");
// Insertion sort algorithm
for (int i = 1; i < list.length; i++) {
int currentValue = list[i];
int j = i - 1;
// Shift larger elements to the right
while (j >= 0 && list[j] > currentValue) {
list[j + 1] = list[j];
j--;
}
// Place the current value in the correct position
list[j + 1] = currentValue;
// Print the list after each insertion
for (int k = 0; k < list.length; k++) {
System.out.print(list[k] + " ");
}
System.out.println(); // New line after each pass
}
// Final sorted list
System.out.println("Sorted array:");
for (int num : list) {
System.out.print(num + " ");
}
}
}
InsertionSort.main(new String[]{});
Sorting process:
12 28 18 8 30 3 17 14
12 18 28 8 30 3 17 14
8 12 18 28 30 3 17 14
8 12 18 28 30 3 17 14
3 8 12 18 28 30 17 14
3 8 12 17 18 28 30 14
3 8 12 14 17 18 28 30
Sorted array:
3 8 12 14 17 18 28 30
Insertiona Analysis - Big O
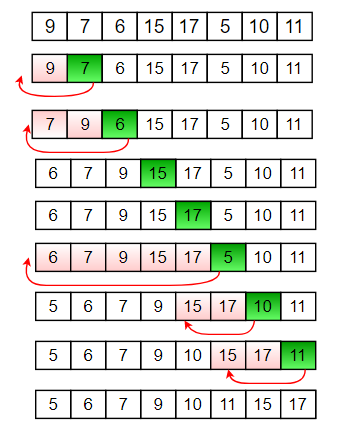

Let $n$ be the number of integers in an array.
Each iteration in insertion sort leads to a new comparison. For example, the first iteration will have $(n-1)$ comparisons, the second will have $(n-2)$, and so on, until the last iteration which will have 1.
Number of comparisons: $(n-1) + (n-2) + \ldots + 1 = \frac{n(n-1)}{2} \approx O(n^2)$
-
Best case: Array is already sorted (only $n-1$ comparisons, $O(n)$ time).
-
Average case: Elements are randomized (about $O(n^2)$ time).
-
Worst case: Array is in reverse order (maximum comparisons and shifts, $O(n^2)$ time).
